フルレバ50倍でFXシステムトレード。

※前回の記事を読んでない方は、先に前回の記事をどうぞ
※もし下記を読んでる途中で書かれてる内容の感じがつかめない時は、ひとまず最後までゆっくり読んでみて、あとでまた改めて読み直した方が分かりやすいかも知れません。（後半には図も出てくるので、イメージ湧きやすいと思います）

■ 負けても半分戻ってくるなら、「増える方法」と「増えない方法」がある

まず、先週の問題を改めて振り返ります。
先週の問題は、要約するとこういう事です。

この答えは、「ちゃんとやればお金は無限に増やせられる」でした。
ただ、やり方を間違えると「お金は増えも減りもしない」になるという事でした。
ここでは噛み砕いて、分かりやすく「勝てる方法」と「勝てない方法」と表現してみます。

で、おさらいですが、勝てない方法というのは「資金＝賭け金」としてしまう賭け方でした。
こうすると「1万円が勝って2万円になっても、そのあと負けたら1万円に逆戻り」です。
永遠に増えません。
このように、2通りの結果があるという事をよく覚えておいて下さい。
お金の掛け方の違い１つで、「増えたり」、「増えなかったり」するということです。

■ 負けて全額失うなら、「減る方法」と「減らない方法」の２つがある

次に、上の問題と似てるけどちょっと違う問題を考えてみます。

…この問題の方が、さっきのより実際のギャンブルに近いですね。
ちなみにこの答えは、「増えも減りもしない」方法と、「減り続ける」方法の2通りに分かれます。
ここではもっと噛み砕いて「負けない方法」と「負ける方法」と表現しておきましょう。

で、まず「負けない」方法はどんなやり方か～ですが、
これは単純に、前回記事の正解例のように「毎回決まった額を賭ける」という方法です。
具体的には、例えば手元に1万円がある場合に1000円ずつ賭けるやり方です。
そうやって賭けると、リターンは

・2分の1の確立で2000円
・2分の1の確立で0円

となります。
「0円が戻ってくる」なんて書くのは変な感じがしますが、書き方を統一すると見えてくる事もあるので、こうしておきます。
ちなみに、上の二つの結果は言い方を変えるとこういう事です。

・2分の1の確立で1000円増える
・2分の1の確立で1000円減る

つまり、増えても1000円。減っても1000円。
その確立が一緒なのだから、永久に変わらない。お金は増えない。でも減らない。そういう事ですね。

という訳で、「負けない方法」が分かりました。
次に、先ほど書いた「負ける方法」ですが
これは単純に、「手持ち資金の10%で賭ける」というような賭け方です。
もうちょっと言うと「掛け算を使って賭け金を決める方法」です。
為替のレバレッジなんかはこういう考え方ですが、掛け算使ったら絶対減ります。
どう減っていくのか、確認してみましょう。

まず、例えば『賭け金は常に資産の10%』と決めます。
資産 x 0.1 です。
だから、例えば手元に1万円あったとすると、最初の賭け金は1000円。
そしてその1000円は、

・2分の1の確立で2000円
・2分の1の確立で0円

になって戻ってきます。
ここまではまだ、先ほどと同様ですね。
ただ、この「手持ちの10%」というやり方は、1回目のゲームの勝敗によって2回目のゲームの賭け金が変わるのがミソです。
勝ったら次の賭け金も大きくなって、負けたら次の賭け金は小さくなります。
という訳で、複数回やるとどうなるかを見定めないといけません。
なので、ここでは仮に2回ゲームをやった時の
「負けたあと勝つ」、「勝ったあと負ける」という、それぞれのケースを考えてみます。
すると

と、どちらも9900円へと減ってしまいます。
言い換えると、2回ゲームする事で1%減るという事です。
だから、こういうやり方をすると減り続けます。
つまり、「負ける方法」な訳です。
ゲームをたくさんすれば、どうあがいてもどんどん減っていきます。

■ 「負ける方法」と「負けない方法」の境目はどこにあるのか？

問題なのは、「決まった額を賭け続ける」なら、負けないで現状維持できるのに
なぜ【「手持ちの資金の10%を賭けるやり方」だと減り続けるのか】です。
ここに一つポイントがあります。

これ、先にダメな理由を言ってしまうと、「資金と賭け金が連結してしまう」からダメなんです。
掛け算を使うとダメっていうのは、「資金と賭け金が連動してる」からダメという事です。

そのことをよく理解するために、まず一つ確認ですが、
「パーセント」っていうのは、当たり前ですが掛け算です。

・10%だったら x 0.1
・50%だったら x 0.5

だから、パーセンテージで賭け金を決めると、

・資金が大きくなると賭け金も大きくなる
・資金が小さくなると賭け金も小さくなる

となるわけですが、
こんな風に、「資金の増減によって賭け金も増減する」というのは、
言い換えると、「資金と賭け金が連動している」という事ですね。

こんな事は当たり前なんですが、ここが重要です。

先ほどの、「減らない方法」の方は、「資金と賭け金が連動していない」から、減らなかったんです。
言い換えると、「資金」と「賭け金」というのが、別々の次元に存在していたから減らなかったんです。
一種の2重構造です。
しかし、あいだに掛け算を使うと、それによって別々の次元に存在していた「資金」と「賭け金」がいっしょになってしまう。
だから、賭け金を決める計算式に「資金 x 0.1…」などとどこかに掛け算を使った時点で、
どうやったって、お金は減っていきます。
掛け算の方が足し算よりスマートでクールで上級な感じしますけど、
掛け算使って賭け金を決めると、その時点で負けちゃいます。
掛け算の方が偉いなんて事はないんです。

--

―で、ここで先週出した最初の問題、『倍か半分になる問題』の答えを思い出してください。
答えには2つありました。
「無限に増やせる方法」と「増えも減りもしない方法」です。
それらの違いは、
・資金と賭け金が別々なら「無限に増やせる」
・資金＝賭け金だと、「増えも減りもしない」
でした。

で、こうやって2つの問題の2通りの答えを並べると、『なんだかどちらの問題の答えも、その違いの構図が似てるな』という事に気づきますね。
少しまとめてみます。

上のそれぞれ下の行の、「一緒」と「連動」というのが、同列の似通ったものなんだと認識するのが大事です。
この2つが、「分離」という考え方の対になっています。
ただ、上の問題と下の問題で、対の成り立ち方がちょっと違うんですが、とにかく対になっているんだ、というのが肝心なとこです。

で、両方の問題の答えの共通点の「分離」という事についてですが、これは
「完全に分離された資金の括りが、外側に一つ用意されている」という状態を表しています。
･･･が、まだピンと来ないかも知れないので、少し図を交えてみます。

まず、賭け金と資産が別の次元になってるイメージ図です。

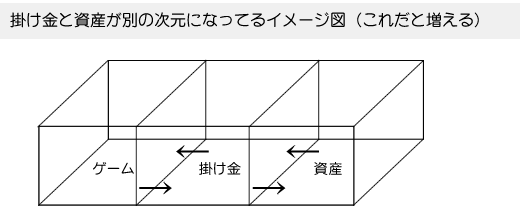
全部別々の部屋（階層）になってるのがミソです。
これだと、『2分の1の確立で倍か半分になる』問題でも、『2分の1の確立で倍かゼロになる』問題でも
資産が減る事はないです。
ここではわかりやすく「負けない方法」と呼ぶことにします。

次に、賭け金の決め方に掛け算を使ってしまい、賭け金が資産と連動する場合のイメージ図です。

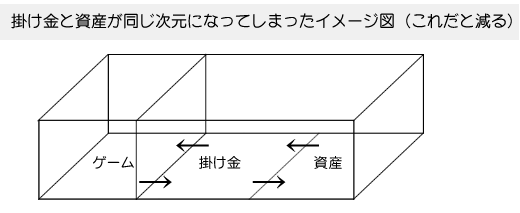
掛け算を使うと、賭け金と資産の部屋の敷居がなくなってしまい
同じ次元へと結びついてしまう感じです。
これだと、『2分の1の確立で倍か半分になる』問題では増やせるのに増やせない事になったりし、
『2分の1の確立で倍かゼロになる』問題では確実に減っていきます。
ここではわかりやすく「勝てない方法」と呼ぶことにします。

で、どちらの問題にも共通するのは、『とにかく、「資産」と「賭け金」が別の部屋になっていればいいんだよ』、って事です。そうすれば、増える事はあっても減る事はありません。これが負けない方法です。
これがここまで「分離」と表現してきたことです。
…まぁ先週出した１つめの問題の方は、資産より賭け金がある程度小さければ連動してても増えちゃうんですが。
（気になる人は計算してみてください。）

ここで少し脱線しますが、掛け算というのは2つのモノを結びつけてそれらを一緒の次元として扱う記号なんだと思います。
速さ x 時間 = 距離 や、 電流 x 電圧 = 電力 とか、それこそ 縦 x 横 = 面積 もそうですね。
掛け算をすると、2つが結びついてそこに全く新たな一つの評価軸や空間が構築されるようなイメージです。
だから、構造を多層にしたい場合は、掛け算をせず、足し算や引き算で値を渡すべきなんだと思います。

例えば、先週の問題の解答の、「500円賭けて勝ったら500円手元に戻し、負けたら手元から250円補充する」というやり方は、
手元のお金と賭け金の関係が、足し算と引き算でしか結びついてないですね。
そして同じく今日の、『2分の1で倍かゼロになるゲーム』の「資産が減らない賭け方」というのは、
「500円賭けて勝ったら500円手元に戻し、負けたら手元から500円補充する」と言い表せるので、
やっぱり手元のお金と賭け金の関係は、足し算と引き算でしか結びついてないわけです。
ここがポイントです。
ここの関係に掛け算を使っちゃうと、『倍かゼロになる問題』はどうやったってお金が減っていきます。
2つの次元が結びついちゃうんですね。

…掛け算って足し算の複数形なだけなのに、不思議なもんです。

ちなみに、構造を多層にする事で解ける問題というのは、コップの中身入れ替えなどがありますね。
赤い水が入ったコップAと、青い水が入ったコップB。この中身を入れ替えるには
そのままだと、幾ら考えてもどうやったって解けないですが、コップCを持ってきたら解けますね。
そんな感じで、多層にする事で解決する問題っていうのは多いんだと思います。
先週の問題を解こうとして、最初に「増えも減りもしない」と何となく感じた人は、コップAとコップBだけで考えようとしたから、そう感じたわけです。
そして、前回の正解例のように、「賭け金とは異なる"資産"っていう入れ物を持ってきて考える」と解決する訳ですが、これはつまりコップCという入れ物を持ってきて考えるのと同じことです。

コップの中身入れ替えの話はちょっと飛躍してるように見えるかもしれないですが、かなーり似てます。次に進むとその辺りがもっとわかります。

--

上記の「部屋の区切り」の考え方を踏まえつつ、それは一旦置いておいて、シストレ寄りの話題に移ります。

まず、今回書いてきた内容がシストレにおいて最もダイレクトに影響するのは何か？ ですが、
それは恐らく、年間パフォーマンスの捉え方でしょう。
普段のトレード単体では、あんまり関係がありません。
なにせ普段のトレードというのは、勝ったら増えるけど負けたらマイナスなのであって、「負けても半分戻ってくる」なんてウマイ話しはないので、あんまり関係ありません。
ただ、そんな普段のトレードも、その勝ち負けを口座のパーセンテージとして捉えると話が変わってきます。
具体的には、例えばレバ25倍で40pips勝つか負けるとしたら、それはちょうど口座の10%の増減になりまよすね。
そんな感じで、トレード単体を見るのではなく、トレードの結果で口座がどう増減していくか、その推移を見て行きます。
そうすると、毎年、年の終わりには「口座の年間パフォーマンス」なんてものが、書き表せますね。
もしかするとそれが、

・2分の1の確立で口座残高が倍になる
・2分の1の確立で口座残高が半分になる

という事は充分ありえます。
というかこんなシステム、全然大したことないわけです。
このシステムじゃ口座のお金は増えも減りもしないんですから。全然ダメなシステムです。

―が、しかし。

この口座という全ての元締めの更に外側にもう一つ大きなくくりを用意してやります。
そうすると上のシステムが無限にお金を増やせる仕組みになるわけです。
構造を多層にさえすれば、横の分散投資なり、縦の分散投資なりでお金は無限に増やせる、という事です。

言葉だけだとわかりにくいので、再び図を交えます。

まず、「年間パフォーマンス」って考え方の正体から考えます。
通常のトレードシステムの評価の仕方というのは、こういう構図だと言えます。

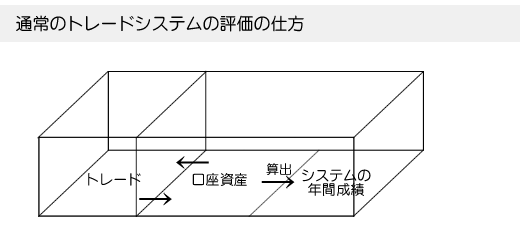
『年率20%の…』などと、パーセンテージでシステムの成績を表した時点で
口座資産とシステムの成績は、同じ次元のことを表しているに過ぎません。
こう書くと堅苦しいですが、口座が100万→120万と推移する事を、「+20%」と置き換える計算が
「システムを評価する」という事だよ、と言ってるに過ぎません。
プロフィットファクターや連勝/連敗、ドローダウンなんかも、そういった口座の数字の変化を
人間にとって意味あるデータに変換してるだけですね。

で、仮にここに、具体的にとあるシステムがあり
それを運用するとこんな感じに口座残高が推移するとします。

『100万→200万→100万→50万→100万→200万→100万…』

これはつまり

・2分の1の確立で倍
・2分の1の確立で半分

という成績のシステムと呼べるわけで、この場合、この口座のお金は永遠に増えそうにないわけです。
このまま未来永劫、時に増えたり時に減ったりしながら、100万前後をうろうろする事になるでしょう。

―が、しかし。

そんなふうに口座のお金を永遠に増やせそうにないシステム（トレードルール）も
次の図のように、外側にひとつ大きなくくりを用意した上で、並行して同時に使うと…

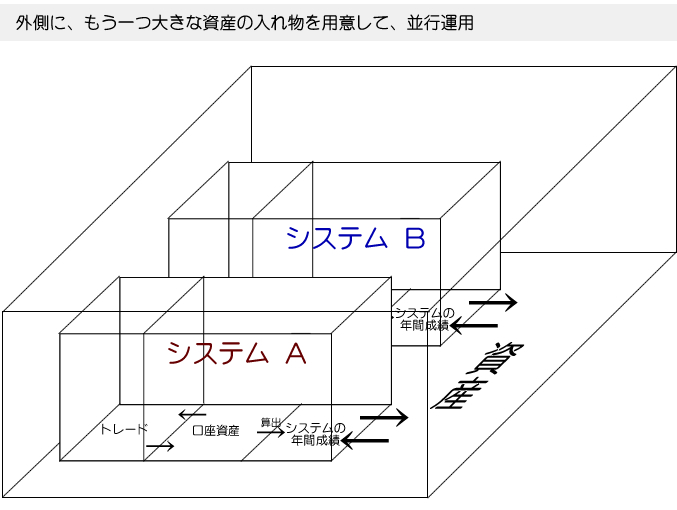
こうすると、無限にお金が増える打ち出のこづちとなるわけです。(※相関性がない必要がありますがその説明は省略）

―…ともかく実際に計算して確認してみましょう。

このように、口座のお金を永久に増やせそうになかったシステムも、
外側に一つ大きな括りを用意すると、無限にお金を増やせる仕組みになる。
また、このような並行運用が無理で、同時に1つしかシステムが使えなくとも
前回説明したように、時系列上に並べて「縦の分散投資」をすれば、上の例と全く同じように125万円に増やせます。
（時間は倍かかっちゃいますが）

--

とまぁこういう事です。

まとめるとつまり、普段のトレードだと「負けたのに半分戻ってくる」なんてパーセンテージな事はないですが、
トレードの勝ち負けの結果を、口座全体のパーセンテージの変化として捉えると、トレードの勝ち負けがパーセンテージの世界になるわけです。
そして、何か一定のトレードルール（システム）でトレードしたとして、その年間のパフォーマンスが

・2分の1の確立で倍
・2分の1の確立で半分

なら、口座のお金自体はそのままだと増えも減りもしないけど、更にその外側にもう一つ大きなくくりを用意してやれば
今度はお金が毎年1.25倍になる立派なシステムになる。

これは、極端な話し↓こんなシステムでもお金が増える事を示してます。

これ、勝ちのリターンが微妙なわりに、おっそろしく派手な負け方してるシステムですね。
ちなみに「90%減」っていうのは、100万のうちの90万がなくなるという事で、資産が10分の1になるという事です。
10回の内もし最初の2回でこの負けが連続したら、100万が一気に1万になっちゃう訳ですね。
だから、仮にそこからたかだか30%が8回連続したとしても、焼け石に水。
一応、30%複利の威力で1万→8万円ほどにまで回復しますが、結局元の100万円は8万円になり、92万円も減ってしまった訳でもう悪夢としか言えない。
当然、こんなシステムを自分の口座で運用していたら、あっという間に資産は吹っ飛んで泣くハメになるでしょう。
でも、その口座残高の外側にもう一つおおきな「資産」という括りを用意して、その「資産」からの一部で口座を運用する…という多層構造で考えれば
増えるんです、こんな劣悪なシステムでも。
まぁ100万円が106万円に増えるだけですけど、でもちゃんと6%増えるんです。このダメダメなシステムでも。

…と、理屈がわかってもまだ不思議な感じですね。
でも折角なので、この現象の本質をよりはっきりさせてみましょう。
上のシステムをさらに悪化させ、わかりやすく以下のようにします。

2割の確立でいきなり破産します。凄いぶっ飛びようです。
…でも、ここまで酷いシステムだとしても、まだ増えます。
つまり、『資産がゼロになっちゃったら、もうおしまいじゃん、そんな破産システム使えないじゃん』ではないという事を
今回の問題とその解答は示してるわけです。

ちなみに、この2割で破産するシステムは、こう文章を置き換えるとわかりやすいです。

80% の確立で、賭け金の 1.3倍が戻ってくる
20% の確立で、賭け金が ゼロになる

「資産」を「賭け金」に置き換えて書きましたが、こう書くと、「賭け金とは別に、その賭け金の元になってる資産があるんだな」
ってのが自然と分かりますね。日本語って便利です。

だから上記の2割破産システムも、例えばそれが一つのゲーム機だと考えて、それが10台あったとして計算すると
手持ちの100万円を10万円ずつで投資すれば

・8台に賭けた80万円が104万円に
・2台に賭けた20万円が0円に

という訳で、4万円増える訳です。
勿論、ゲーム機が複数台なかったとしても問題ありません。
前回説明した、「縦の分散投資」を使えば1台のゲーム機でも同じく4万円増えます。

--

という訳で、こんな破産システムなんて普通に口座で運用したらボロボロですけど、
構造を多層にするだけで、増える仕組みになってしまうわけですね。

この事が、あまり今までのシストレの世界では語られてなかったんではないかな、と思って
前回の問題を作ってみた、ということでした。

--

…で、最後にまとめですが
思うにコップの中身入れ替え問題もそうですけど、今回のように多層や並列にすると解決するという問題は沢山あるんだと思います。
何か困ったことがあれば、「区切りを作って、その外側にそれを含むもう１つ大きな括りの入れ物を考える」
とやってみるといいかも知れません。
上手くいくケースは、他にもたくさんあると思います。
それこそ、システム内部のトレードのルール作りにも使えるかも知れないですね。